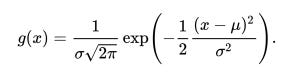The Drunkard’s Walk
I decided to re-read one of my favorite books about statistics recently, because I’ll be teaching stats this year at the Gokhale Institute.
The Drunkard’s Walk is a book written by Leonard Mlodinow, and it is a fun, engaging and light read. The first and the third of those adjectives, I admit, will only be used by folks who have spent a lot of time teaching or learning statistics. Why is that? Because most stats syllabi seem intentionally designed to be anything but the second of those adjectives.
And so most of us treat stats as a subject that needs to be passed in college, rather than a fascinating way to help us make sense of the world around us. But that is precisely why one should read books like this one – because you begin to understand the ways in which you can apply ideas from statistics to the world around us.
If you read that last sentence again, you will see that I have used the word ‘ideas’, as opposed to ‘formulas’. The distinction matters, at least to me, because in our misguided efforts to impart rigor to the subject, we often end up sacrificing intuition.
The Pain Point
I can (and have) wax lyrical about the properties of this formula in class. But it is important to remember while doing so that the point is, as always, to answer the question: TMKK?
What, for example, is the TMKK of the symmetric nature of the bell curve? Consider this lovely little story, taken from the book:
Decades later the great French mathematician Jules-Henri Poincaré employed Quételet’s method to nab a baker who was shortchanging his customers. At first, Poincaré, who made a habit of picking up a loaf of bread each day, noticed after weighing his loaves that they averaged about 950 grams instead of the 1,000 grams advertised. He complained to the authorities and afterward received bigger loaves. Still he had a hunch that something about his bread wasn’t kosher. And so with the patience only a famous—or at least tenured—scholar can afford, he carefully weighed his bread every day for the next year. Though his bread now averaged closer to 1,000 grams, if the baker had been honestly handing him random loaves, the number of loaves heavier and lighter than the mean should have—as I mentioned in chapter 7—diminished following the bell-shaped pattern of the error law. Instead, Poincaré found that there were too few light loaves and a surplus of heavy ones. He concluded that the baker had not ceased baking underweight loaves but instead was seeking to placate him by always giving him the largest loaf he had on hand. The police again visited the cheating baker, who was reportedly appropriately astonished and presumably agreed to change his ways.
Mlodinow, Leonard. The Drunkard’s Walk: How Randomness Rules Our Lives (p. 188). (Function). Kindle Edition.
Let us be frank and admit that Poincare was being a little so-and-so. Or at any rate, one might sympathize with this being the baker’s chief opinion of one of the greatest mathematicians of his time.
But consider, at the same time, the fact that Poincare was in essence applying the TMKK principle to his daily life! He wasn’t being a little so-and-so in terms of demanding perfection – the point wasn’t to walk away with a loaf that would weigh exactly a Platonic 1000 grams each day.
Errors, he knew, were inevitable, and that was just fine with old Jules-Henri. But ah, the errors weren’t randomly distributed! What were the chances that he’d almost always get a heavy loaf of bread if the errors were randomly distributed? On half the days in that fateful year, he should expect to get bread a little bit lighter than 1000 grams, and the other half of the year, that loaf should be a little bit heavier than 1000 grams. Mota-moti, as the wonderfully evocative phrase goes, that is what one should expect.
And the fact that this is not happening meant – all but guaranteed – that the baker wasn’t randomly picking up any old loaf and handing it to Poincare. The baker was deliberately picking up the heaviest loaf he could find – because he knew that the other loaves were all less than 1000 grams.
(I’m worried that you, dear reader, might miss the pun implicit in this section’s heading, so please do not forget to chuckle before you move on.)
TMKK?
Statistics isn’t about the memorization of formulae and the looking up of tables. I mean sure, for some of us that is a major part of what statistics is. I absolutely should be torturing my students about exponentials and concave quadratic functions.
But I should also absolutely be telling them, at great length and with great relish, the story of that little so-and-so mathematician and his pain.
And if you do not currently find yourself enrolled in a stats course that requires you to know who Weierstrass was and what he was up to, well, lucky you. You can just read about Poincare and all the other lovely stories in Mlodinow’s book and have a great time.
And I strongly recommend that you do – the book is certainly worth your time. And oh, keep an eye out for both the Monty Hall explanation, and the girl named Florida explanation if you do. Superb little takes!